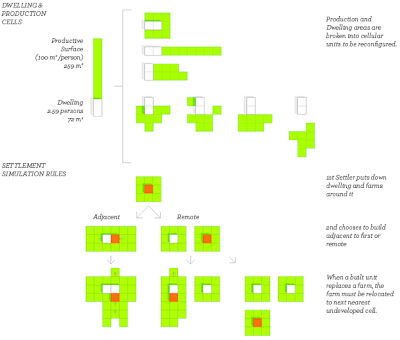
Overview
The Settlement Simulation is a computational model based on a multi-state cellular automata. The model uses simple behavioural rules to recreate the aggregation logic of dwellings and small subsistence farms in a given area via an ‘unplanned’ vernacular methodology. The goal of the simulation was to investigate the sorts of distributions and collective form that might result without the oversight of a top-down ‘planner’.
Computational Rules
The simulation beings with the first ‘settler’ arriving on site placing his/her dwelling and farming the land around it. The dwelling has a footprint of 72 m2 (6m x 12m), based on a typical urban townhouse in the northern latitudes. The household size is considered to be 2.59 persons. The ‘farmed’ area attached to the dwelling is 100 m2/person (259 m2/household).
A second settler arrives and ‘randomly’ chooses to build either adjacent to the first or to build remotely. Should they build adjacent, they need to relocate any farm land displaced by their dwelling. If remote, they will potentially begin a new settlement. This process is repeated until the field is full.
In the computational model these dwellings and farms are broken into modular units. The dwelling area is represented as one unit while the associated productive area required is approximately equal to the area of three dwelling units. Therefore, with every one dwelling placed, three productive units must be placed.
The likelihood for a new settler to build remote or adjacent is weighted by a ‘Friendliness Factor’ (F), a number between 0 and 1. F = 0 means all units will try to build remote, while F = 1 means all units will try to be attached. An F of 0.3 results in a 30% chance that a unit will choose to build remotely.
Vertical growth is triggered when a settler ‘chooses’ to build on an existing dwelling in a settlement which is sufficiently dense. In computational terms, this means that when the ‘state’ of the selected cell is already set as a dwelling, the neighbouring cells are checked to see how many surrounding cells are also dwellings. If the count of neighbour dwellings is above the given vertical growth threshold (v), a dwelling is added to that cell (presumably another flat above the existing). If the number of neighbours is less than (v), the agent chooses one of the unbuilt cells to build on.
Parameters
(F) Friendliness Factor: variable from 0 to 1
Controls likelihood of dwellings to cluster and therefore size of resulting dwelling clusters
(A) Field Size: 1 km2
The simulation was run on an area of 1 km2 in order to limit the distribution of dwellings and farms to an area considered ‘walkable’.
(v) Vertical Growth threshold: 8 (range: 0 - 8)
Number of surrounding dwellings needed to trigger vertical growth
(PI) Production Intensity: 1person = 100m2
(Dw) Dwelling/Household size: 72m2 = 2.59 persons
Qualities Measured
(Dp) Population Density:
Measured at two scales - density of the overall tissue, as well as locally for the dwelling clusters.
(H) Floor Height:
Both maximum and average floor heights are measured in each tissue generated.
(OSR) Open Space Ratio:
The ratio of unbuilt ground area to built volume.
Method & Observations
(11) tissues were generated, starting with an F value of 0 and increasing in steps of 0.10 with each run. Population density distribution was measured in each tissue using a scanline analysis. For every scanned line of cells (1 cell wide in x-direction, 100 cells long in y-direction) the number of dwelling units are counted and divided by the overall total. This gives us the percentage of dwellings in each row. Frequencies were plotted and used to compare how Friendliness affects the heterogeneity of the generated tissues.
Method & Observations
(11) tissues were generated, starting with an F value of 0 and increasing in steps of 0.10 with each run. Population density distribution was measured in each tissue using a scanline analysis. For every scanned line of cells (1 cell wide in x-direction, 100 cells long in y-direction) the number of dwelling units are counted and divided by the overall total. This gives us the percentage of dwellings in each row. Frequencies were plotted and used to compare how Friendliness affects the heterogeneity of the generated tissues.
‘Friendliness’ = 0 resulted in a relatively homogeneous distribution of dwellings and farms as agents try to distance themselves from each other by choosing random positions in the field. The resulting tissue resembled a suburban settlement typology where distancing is the predominant spatial characteristic.
‘Friendliness’ = 1 resulted in one large cluster of dwellings with agriculture constantly being pushed outwards and eventually becoming one large productive area surrounding a single dwelling cluster. This resembles a low resolution model of the current urban/agriculture dynamic whereby intensive development in cities pushes food production out of any land within a desirable travel distance to the city centre.
As we moved incrementally from F=0 to F=1 we observed the dwelling clusters growing in density and size, allowing for larger identifiable agricultural areas to form in the field.
When F=0.7 to F=0.9, we see dwellings primarily tending to cluster with the occasional ‘loner’ breaking from the group to become a seed for a new dwelling cluster. The earlier in the simulation the dwelling is placed, the larger the resulting cluster. The resulting tissue contains a range of cluster sizes resembling a distribution of settlements in an urban region. Christopher Alexander suggests that settlement sizes will follow Zipf’s law resulting in varying sizes.
Population Density ranges from 64.75 when F = 0 to 75.55 when F = 1. This is to be expected as the total number of people that can live in the given area is limited by the production capacity of a plot which is set at 1 person / 100 m2.
Evaluation & Conclusions
The aggregation patterns that emerge from the Settlement Simulation suggest human settlement patterns at several scales higher than explicitly intended in the setting out of the model rules. This suggests that perhaps by limiting the distance to which a community is allowed to relocate its agriculture, we might introduce a fractal nature to the organisation of our urban area where the pattern at the neighbourhood scale is similar to the pattern at the regional scale.
We may take advantage of the increasing heterogeneity of the tissues of increasing F values in order to work between various scales. By using higher F values tissues may be more appropriate as a low resolution pattern for a larger scales while the more homogenous lower F values might be better suited to create higher resolution tissues to be used at the neighbourhood scale.
In subsequent development we will introduce (D) Population Density targets. This will require increasing productivity of agricultural plots as well as incorporating area for infrastructure and public space within the simulation. In order for it to be meaningful (D) should be measured as a gross density as opposed to a net density.